24. The Solow-Swan Growth Model#
In this lecture we review a famous model due to Robert Solow (1925–2023) and Trevor Swan (1918–1989).
The model is used to study growth over the long run.
Although the model is simple, it contains some interesting lessons.
We will use the following imports.
import matplotlib.pyplot as plt
import numpy as np
24.1. The model#
In a Solow–Swan economy, agents save a fixed fraction of their current incomes.
Savings sustain or increase the stock of capital.
Capital is combined with labor to produce output, which in turn is paid out to workers and owners of capital.
To keep things simple, we ignore population and productivity growth.
For each integer
The function
Production functions with this property include
the Cobb-Douglas function
the CES function
Here,
We assume a closed economy, so aggregate domestic investment equals aggregate domestic saving.
The saving rate is a constant
Capital depreciates: without replenishing through investment, one unit of capital today
becomes
Thus,
Without population growth,
Setting
With
Our aim is to learn about the evolution of
24.2. A graphical perspective#
To understand the dynamics of the sequence
To do so, we first
need to specify the functional form for
We choose the Cobb–Douglas specification
The function
Let’s define the constants.
A, s, alpha, delta = 2, 0.3, 0.3, 0.4
x0 = 0.25
xmin, xmax = 0, 3
Now, we define the function
def g(A, s, alpha, delta, k):
return A * s * k**alpha + (1 - delta) * k
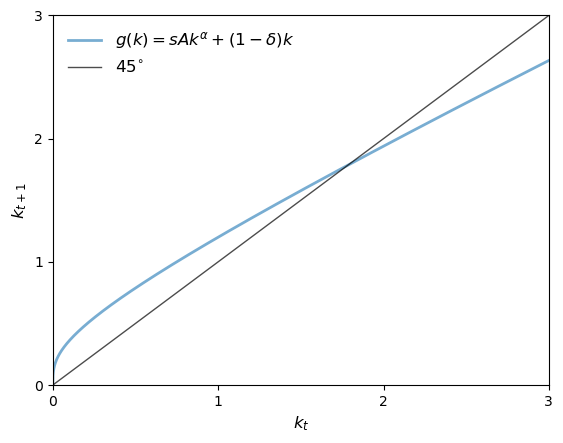
Let’s plot the 45-degree diagram of
def plot45(kstar=None):
xgrid = np.linspace(xmin, xmax, 12000)
fig, ax = plt.subplots()
ax.set_xlim(xmin, xmax)
g_values = g(A, s, alpha, delta, xgrid)
ymin, ymax = np.min(g_values), np.max(g_values)
ax.set_ylim(ymin, ymax)
lb = r'$g(k) = sAk^{\alpha} + (1 - \delta)k$'
ax.plot(xgrid, g_values, lw=2, alpha=0.6, label=lb)
ax.plot(xgrid, xgrid, 'k-', lw=1, alpha=0.7, label='$45^{\circ}$')
if kstar:
fps = (kstar,)
ax.plot(fps, fps, 'go', ms=10, alpha=0.6)
ax.annotate(r'$k^* = (sA / \delta)^{(1/(1-\alpha))}$',
xy=(kstar, kstar),
xycoords='data',
xytext=(-40, -60),
textcoords='offset points',
fontsize=14,
arrowprops=dict(arrowstyle="->"))
ax.legend(loc='upper left', frameon=False, fontsize=12)
ax.set_xticks((0, 1, 2, 3))
ax.set_yticks((0, 1, 2, 3))
ax.set_xlabel('$k_t$', fontsize=12)
ax.set_ylabel('$k_{t+1}$', fontsize=12)
plt.show()
<>:15: SyntaxWarning: invalid escape sequence '\c'
<>:15: SyntaxWarning: invalid escape sequence '\c'
/tmp/ipykernel_6933/3107437576.py:15: SyntaxWarning: invalid escape sequence '\c'
ax.plot(xgrid, xgrid, 'k-', lw=1, alpha=0.7, label='$45^{\circ}$')
Suppose, at some
Then we have
If
If
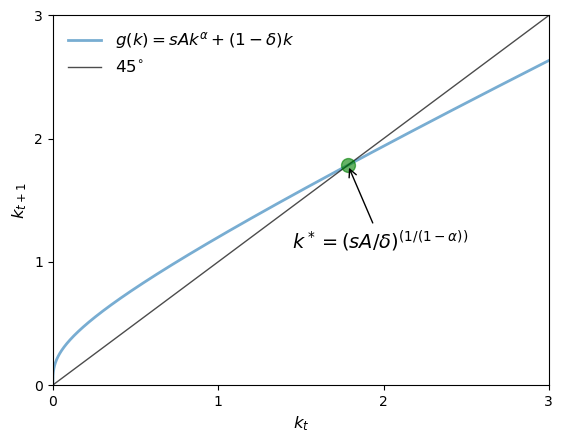
(A steady state of the model is a fixed point of the mapping
From the shape of the function
It solves
If initial capital is below
If initial capital is above this level, then the reverse is true.
Let’s plot the 45-degree diagram to show the
From our graphical analysis, it appears that
This is a form of global stability.
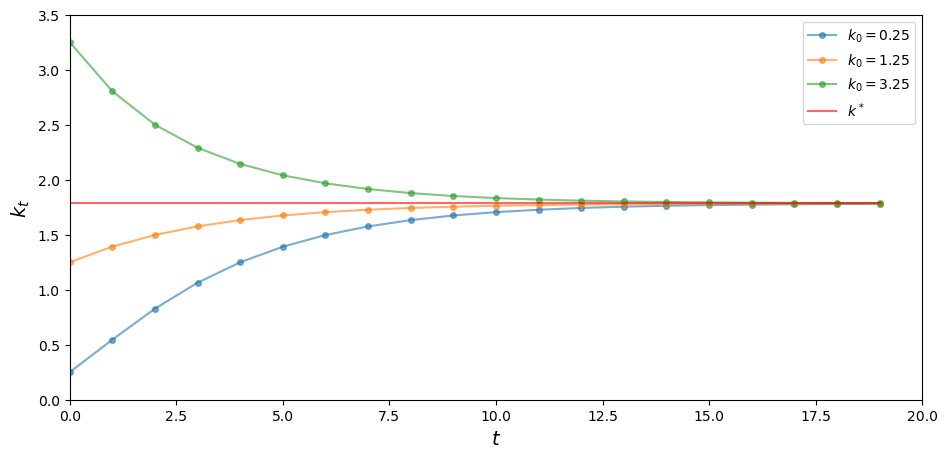
The next figure shows three time paths for capital, from three distinct initial conditions, under the parameterization listed above.
At this parameterization,
Let’s define the constants and three distinct initial conditions
A, s, alpha, delta = 2, 0.3, 0.3, 0.4
x0 = np.array([.25, 1.25, 3.25])
ts_length = 20
xmin, xmax = 0, ts_length
ymin, ymax = 0, 3.5
def simulate_ts(x0_values, ts_length):
k_star = (s * A / delta)**(1/(1-alpha))
fig, ax = plt.subplots(figsize=[11, 5])
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ts = np.zeros(ts_length)
# simulate and plot time series
for x_init in x0_values:
ts[0] = x_init
for t in range(1, ts_length):
ts[t] = g(A, s, alpha, delta, ts[t-1])
ax.plot(np.arange(ts_length), ts, '-o', ms=4, alpha=0.6,
label=r'$k_0=%g$' %x_init)
ax.plot(np.arange(ts_length), np.full(ts_length,k_star),
alpha=0.6, color='red', label=r'$k^*$')
ax.legend(fontsize=10)
ax.set_xlabel(r'$t$', fontsize=14)
ax.set_ylabel(r'$k_t$', fontsize=14)
plt.show()
As expected, the time paths in the figure all converge to
24.3. Growth in continuous time#
In this section, we investigate a continuous time version of the Solow–Swan growth model.
We will see how the smoothing provided by continuous time can simplify our analysis.
Recall that the discrete time dynamics for capital are
given by
A simple rearrangement gives the rate of change per unit of time:
Taking the time step to zero gives the continuous time limit
Our aim is to learn about the evolution of
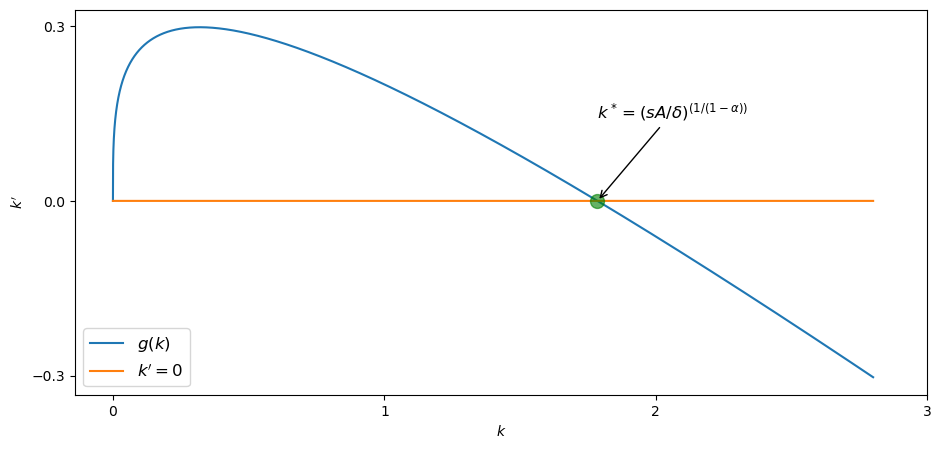
A steady state for (24.3) is a value
We assume
The solution is the same as the discrete time case—see (24.2).
The dynamics are represented in the next figure, maintaining the parameterization we used above.
Writing
When
To see this in a figure, let’s define the constants
A, s, alpha, delta = 2, 0.3, 0.3, 0.4
Next we define the function
def g_con(A, s, alpha, delta, k):
return A * s * k**alpha - delta * k
def plot_gcon(kstar=None):
k_grid = np.linspace(0, 2.8, 10000)
fig, ax = plt.subplots(figsize=[11, 5])
ax.plot(k_grid, g_con(A, s, alpha, delta, k_grid), label='$g(k)$')
ax.plot(k_grid, 0 * k_grid, label="$k'=0$")
if kstar:
fps = (kstar,)
ax.plot(fps, 0, 'go', ms=10, alpha=0.6)
ax.annotate(r'$k^* = (sA / \delta)^{(1/(1-\alpha))}$',
xy=(kstar, 0),
xycoords='data',
xytext=(0, 60),
textcoords='offset points',
fontsize=12,
arrowprops=dict(arrowstyle="->"))
ax.legend(loc='lower left', fontsize=12)
ax.set_xlabel("$k$",fontsize=10)
ax.set_ylabel("$k'$", fontsize=10)
ax.set_xticks((0, 1, 2, 3))
ax.set_yticks((-0.3, 0, 0.3))
plt.show()
This shows global stability heuristically for a fixed parameterization, but how would we show the same thing formally for a continuum of plausible parameters?
In the discrete time case, a neat expression for
In continuous time the process is easier: we can obtain a relatively simple
expression for
The first step is
to set
Substituting into
This equation, which is a linear ordinary differential equation, has the solution
(You can confirm that this function
Converting back to
Since
Thus, global stability holds.
24.4. Exercises#
Exercise 24.1
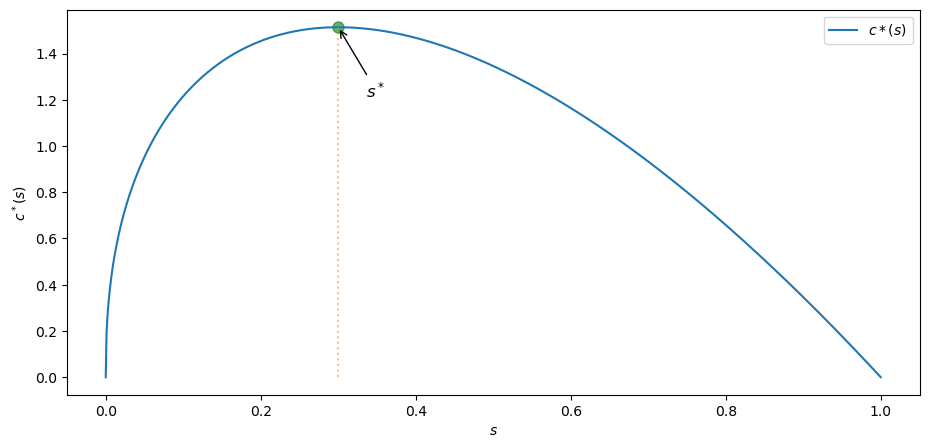
Plot per capita consumption
Use the Cobb–Douglas specification
Set
Also, find the approximate value of
Solution to Exercise 24.1
Steady state consumption at savings rate
A = 2.0
alpha = 0.3
delta = 0.5
s_grid = np.linspace(0, 1, 1000)
k_star = ((s_grid * A) / delta)**(1/(1 - alpha))
c_star = (1 - s_grid) * A * k_star ** alpha
Let’s find the value of minimize_scalar finds the minimum value.
from scipy.optimize import minimize_scalar
def calc_c_star(s):
k = ((s * A) / delta)**(1/(1 - alpha))
return - (1 - s) * A * k ** alpha
return_values = minimize_scalar(calc_c_star, bounds=(0, 1))
s_star_max = return_values.x
c_star_max = -return_values.fun
print(f"Function is maximized at s = {round(s_star_max, 4)}")
Function is maximized at s = 0.3
x_s_max = np.array([s_star_max, s_star_max])
y_s_max = np.array([0, c_star_max])
fig, ax = plt.subplots(figsize=[11, 5])
fps = (c_star_max,)
# Highlight the maximum point with a marker
ax.plot((s_star_max, ), (c_star_max,), 'go', ms=8, alpha=0.6)
ax.annotate(r'$s^*$',
xy=(s_star_max, c_star_max),
xycoords='data',
xytext=(20, -50),
textcoords='offset points',
fontsize=12,
arrowprops=dict(arrowstyle="->"))
ax.plot(s_grid, c_star, label=r'$c*(s)$')
ax.plot(x_s_max, y_s_max, alpha=0.5, ls='dotted')
ax.set_xlabel(r'$s$')
ax.set_ylabel(r'$c^*(s)$')
ax.legend()
plt.show()
One can also try to solve this mathematically by differentiating
from sympy import solve, Symbol
s_symbol = Symbol('s', real=True)
k = ((s_symbol * A) / delta)**(1/(1 - alpha))
c = (1 - s_symbol) * A * k ** alpha
Let’s differentiate
# Solve using sympy
s_star = solve(c.diff())[0]
print(f"s_star = {s_star}")
s_star = 0.300000000000000
Incidentally, the rate of savings which maximizes steady state level of per capita consumption is called the Golden Rule savings rate.
Exercise 24.2
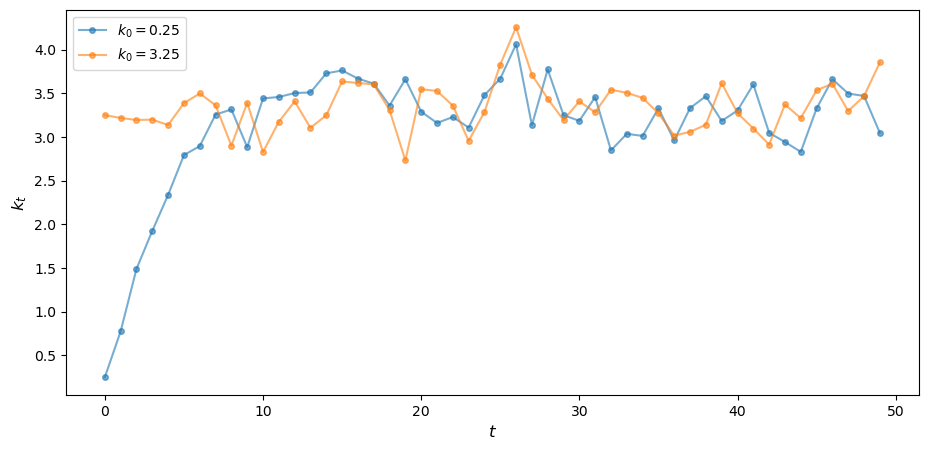
Stochastic Productivity
To bring the Solow–Swan model closer to data, we need to think about handling random fluctuations in aggregate quantities.
Among other things, this will
eliminate the unrealistic prediction that per-capita output
We shift to discrete time for the following discussion.
One approach is to replace constant productivity with some
stochastic sequence
Dynamics are now
We suppose
Now the long run convergence obtained in the deterministic case breaks down, since the system is hit with new shocks at each point in time.
Consider
Generate and plot the time series
Solution to Exercise 24.2
Let’s define the constants for lognormal distribution and initial values used for simulation
# Define the constants
sig = 0.2
mu = np.log(2) - sig**2 / 2
A = 2.0
s = 0.6
alpha = 0.3
delta = 0.5
x0 = [.25, 3.25] # list of initial values used for simulation
Let’s define the function k_next to find the next value of
def lgnorm():
return np.exp(mu + sig * np.random.randn())
def k_next(s, alpha, delta, k):
return lgnorm() * s * k**alpha + (1 - delta) * k
def ts_plot(x_values, ts_length):
fig, ax = plt.subplots(figsize=[11, 5])
ts = np.zeros(ts_length)
# simulate and plot time series
for x_init in x_values:
ts[0] = x_init
for t in range(1, ts_length):
ts[t] = k_next(s, alpha, delta, ts[t-1])
ax.plot(np.arange(ts_length), ts, '-o', ms=4,
alpha=0.6, label=r'$k_0=%g$' %x_init)
ax.legend(loc='best', fontsize=10)
ax.set_xlabel(r'$t$', fontsize=12)
ax.set_ylabel(r'$k_t$', fontsize=12)
plt.show()